Are Jugdral crits better?

[GSC]

Critical hits deal more damage. It’s what they do. Most of you know that normal damage is tripled during a crit, but some might be surprised to hear that it didn’t work like that in the Jugdral games (FE4 and FE5). There, crits double your attack power before subtracting defense.

How does this affect gameplay? To answer this question, we need to dive into the wonderful world of math. Crit damage is calculated like this:

Jugdral Crit Dmg = 2Atk - Def
Normal Crit Dmg = 3Dmg = 3Atk - 3Def

(For simplicity’s sake, I’m gonna call Jugdral Crit Dmg “JCD” and Normal Crit Dmg “NCD” from now on.)

Normally, if you deal no damage to an enemy (your Atk stat is equal to or lower than their Def stat), a crit won’t do anything to help you. After all, 0 x 3 = 0. But that changes in Jugdral. Imagine Atk is 20 and Def is 30. With a crit, Atk becomes 40 but Def stays the same. Result? 10 damage dealt instead of 0.

Jugdral crits help overcome the target’s defenses. They can convert 0 damage into real damage.

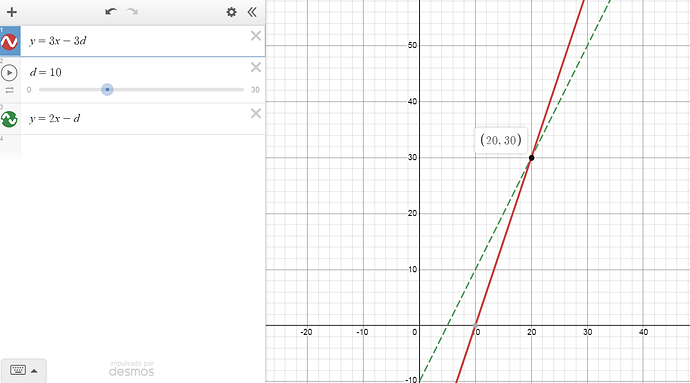
But this doesn’t mean Jugdral crits always deal more damage. Why? Take a look at this graph, where the red solid line represents NCD and the green broken line represents JCD.

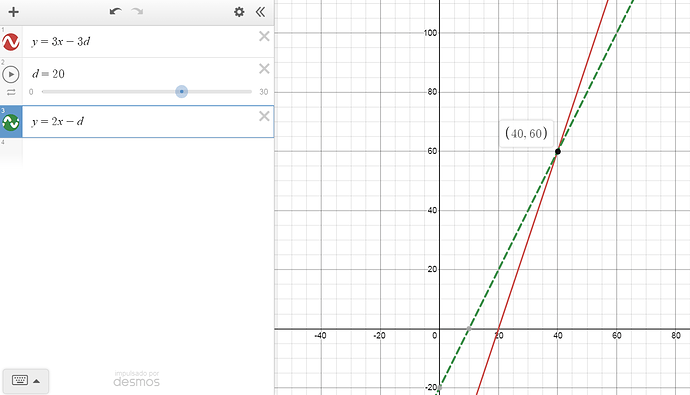
Horizontal axis is Atk, and vertical axis is crit damage. Assuming Def is constant at 10, JCD is higher when Atk < 20, while NCD is higher when Atk > 20. Notice how the trend reverses at 20, which is not a coincidence: it’s Def x 2. For comparison, see the graph when Def is constant at 20:

Here, JCD is higher when Atk < 40, while NCD is higher when Atk > 40. Again, the point of reversal is Def x 2.

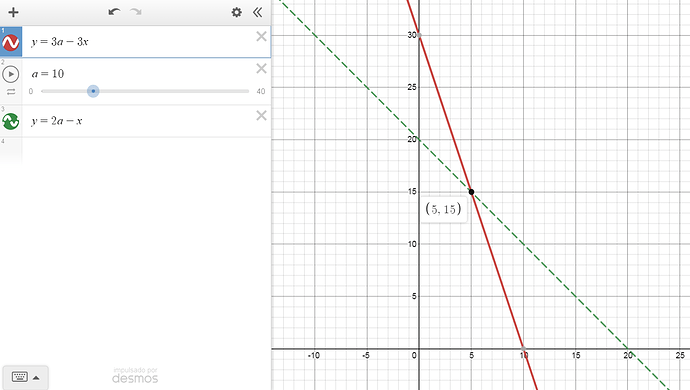
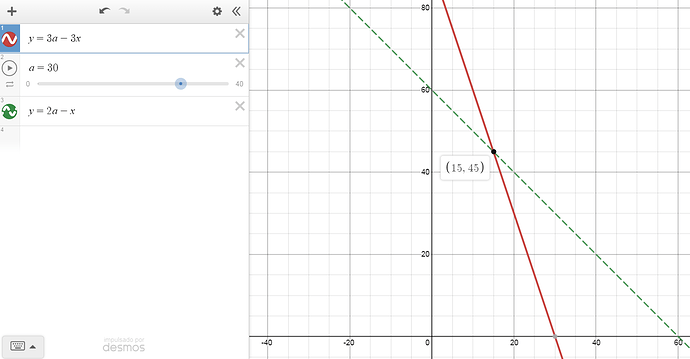
This isn’t the only way to look at the situation, though. We can plot Def against Crit Dmg:

Assuming Atk is constant at 10, NCD is higher when Def < 5, while JCD is higher when Def > 5. If Atk is 30, NCD is higher when Def < 15, while JCD is higher when Def > 15. Point of reversal: Atk / 2.

Finally, we can plot Dmg vs Crit Dmg:

Assuming Def is constant at 0, NCD is always higher than JCD regardless of Atk values. This is because normal crits triple Dmg while Jugdral crits double Dmg and add Def, which is zero in this case. Interesting, but you will rarely see enemies with 0 defense in Fire Emblem, so let’s move on to something more realistic.

Here, Def is constant at 10. JCD is higher when Dmg < 10, while NCD is higher when Dmg > 10. Point of reversal is 10, which is just the Def value. In fact, if you look at the functions, I wrote them specifically as (2Dmg + Dmg) and (2Dmg + Def) to make it clear that, if you want to know which formula gives higher damage, you just need to know whether Dmg is bigger or Def is bigger. A similar graph can be made using Atk as a constant instead of Def, but I like this one because the reversal point is slightly easier to find (the other has the reversal point at Atk/2).

We can also deduce some things with algebra instead of graphs. Jugdral crits deal more dmg when:

2Atk - Def > 3Atk - 3Def
3Def - Def > 3Atk - 2Atk
2Def > Atk

2Atk - Def > 3Dmg
Atk + Atk - Def > 3Dmg
Atk + Dmg > 3Dmg
Atk > 3Dmg - Dmg
Atk > 2Dmg

Now we can summarize how to know under which circumstances one formula yields more damage than the other.

Jugdral crits do more damage when:
· Atk < 2Def
· Def > Dmg
· Atk > 2Dmg

Normal crits do more damage when:
· Atk > 2Def
· Def < Dmg
· Atk < 2Dmg

In layman’s terms, Jugdral crits are better when Dmg is very low. Meanwhile, normal crits either yield low damage if you’re not doing much to begin with, or yield exorbitant amounts of damage if you’re already doing a lot of it. The rich get richer, if you will. Jugdral’s formula is more balanced, and the normal formula is more exaggerated at the extremes.

Jugdral’s formula has serious implications for tanky units. You may think that your armor knight is safe because he takes so little damage from all these enemies. But surprise, this myrmidon just did 15 out of nowhere! Oops. Now high-crit units can pierce through defenses easily. It’s a boon for myrmidons, but a bane for thicc bois.

You might also be wondering, “What about the battle forecast? How are we gonna know how much damage a crit will do? Normally we just multiply dmg by 3, but with Jugdral’s formula we have to multiply atk by 2 and it’s nowhere in the forecast!”

That’s a good point, but! Fire Emblem streamlined damage calculations from FE6 onwards. In Jugdral, the forecast showed the Atk and the Def values, and you had to math out the damage yourself. With the old-fashioned forecast you can deduce JCD easily. If we were to implement Jugdral crits in modern games, though, we should include the possible crit dmg further down the list. In the meantime, you can calculate JCD in modern games by adding Dmg and Atk. A bit cumbersome because it’s not all on the same screen, but it can be done. Alternatively, you can go to Options and change the battle forecast. Now it looks just like in Thracia 776.

In conclusion: the Jugdral games had a formula that benefited those who struggle to do damage, but didn’t produce overkill amounts of it when you were ahead - at least not as much as the normal formula. It makes defensive units worse off and rewards those with high skill. Considering armor knights are seen as underwhelming most of the time, this only digs their grave deeper. If need be, the player can attack the other defensive stat (resistance) to overcome the enemy’s bulkiness. Or the other way around, if it’s a magical enemy with high res. On the other hand, myrmidons are usually underwhelming as well, and this type of crit calculation would make them more useful.

What do you think? Discuss.

(Fun fact: Thabes Labyrinth in Echoes has enemies with almost 100 HP, and you are thankful for the massive amounts of dmg produced by the normal formula. They would be harder to kill with Jugdral’s.)

[Shrimperor]

Imo, No. Especially the way it overcomes high defence i don’t like. Units like Armor units already have alot of trouble to begin with.

But crits in general have never been done well in the series imo. Both 3x Mt and 2xAtk - Def can make a 1% ruin a whole hour of progress.

What i think should be done:

• Reduce crits to 1.5xMt

• Crit classes (like Swordmaster, Berserkers, etc…) and killer weapons get the 3x Damage because it’s a risk reward choice then.

Or

• Disable crits for non-crit classes and weapons.

[Klokinator]

GBA crit be like:
Swordmaster: Tink tink tink death by a thousand cuts
Berserker: Deal 200 damage and overkill literally everything

SNES Crits be like:
Swordmaster: Deal pretty good damage even against armored units
Berserker: Deal pretty good damage even against armored units

Jugdral crits are much better for balance and making crits always good. The real reason you shouldn’t use Jugdral crits has nothing to do with balance though, and more to do with the fact that calculating the damage mid-battle is freaking annoying.

Plus, GBA Swordmaster tink-tink crits are much funnier and we all know memes are best.

[Silver-Star]

I think Jugdral crits ignore Defense or I’m just thinking of the Luna skill.

[Zane]

They do not ignore defense.

Technical details

Battles and their calculations are complex, but consider this snippet that happens while processing FE5’s battle rounds. Highlighted here are a set of subroutines that are run in order, and the things important to crits are where the unit’s might is doubled inside rsActionStructRoundTryProcCrit and where their opponent’s defensive stat is subtracted inside rsActionStructRoundApplyHit.

You’re thinking of Luna, which nullifies the opponent’s defensive stat.

[Permafrost]

One thing to not about crits in FE4 is that, unless I’m forgetting something, I can only think of a few instances where an enemy will be able to crit because crits can only happen because of a skill or a weapon with 50+ uses. The mage sisters and pegasus sisters can get a triangle attack, Tinny/Linda can crit if they get into Wrath range, and Eldigan can crit because of Mystletainn’s Crit skill. So bulky units aren’t really in much danger of getting randomly hit with an attack that overpowers their defenses.

I would say that Jugdral crits work better with FE4’s specific mechanics, but standard crits work better if enemies can crit, so the player can reduce the rate of crit with high Def/Res units.

[theghostcreator]

I much prefer how normal crits work, Jugdral crits, while technically a more useful mechanic just doesn’t really come off as player-friendly, as Shrimperor said armor knights have it bad enough.

Along with that, sometimes players put units in a position and calculate based on stats rather than battle forecast, Jugdral crits aren’t an expected feature and some players may have trouble figuring out how exactly crit damage calculates, just adding to how cumbersome it can be to calculate for damage based on stats and sometimes skills. Plus think about how frustrating it would be to use a unit that would normally take no damage to choke a point only for them to be crit multiple times on enemy phase and die.

Overall I think it’s a good thing the series abandoned Jugdral crit, normal crits are just easier to understand and calculate for.

[GratedShtick]

I actually prefer having SNES critical hits (2Atk) over the normal ones (3Dmg) because it gives units with lower attack a chance to still contribute, even if only by a little. The trick is to make critical hits harder to get, by altering the critical formula to give less from skill or reducing critical given from weapons or supports.

Another neat side effect is that it makes the Hoplon Guard or other critical blocking items have more of a front seat in design where they otherwise wouldn’t.

At least those are my 2 cents.

[Relic]

I think talking about theoreticals is fine and fun, even, but I believe it obscures the actual practical reality of how these mechanics work in the games. I’m not too familiar with the Jugdral games but I’m pretty familiar with gba criticals, at least in the context of hacks. I think that regular crits are better for the calculations aspect alone as has been mentioned, but even past that I think they work better for the game.

People say that low attack units are hurt by it, but why would I be using a swordmaster against an armor with what I presume is an iron sword? The game has a built in solution to this poor matchup and that is to equip an armorslayer and destroy the armor. If low attack units regularly can’t contribute without jugdral crits, then this is an issue unless they’re extremely reliable, and relying on jugdral crits to fix this issue would just homogenize units.

Even then, why not just lower enemy defenses a bit so they’re not doing like 2x2 damage or whatever it is. if they do even something like 6 damage twice, which isn’t a lot, one hit and one crit is 24 damage, which is a very decent amount of damage. Fast and weak units like swordmasters also have the benefit of high speed letting them offset high weapon weight and possibly double with weapons no one else could be doubling with. If other units double the same units with the same or nearly the same consistency, then there’s a deeper problem here than the critical formula.

Of course there’s higher attack units too, which wouldn’t benefit from 3x criticals because they just overkill everything, right? But in practice, this just doesn’t really hold up. Most high strength units are not particularly fast, and don’t even one-hit KO enemies, which means that criticals let them get kills, or if they double, lets them avoid a counter. Even if you were going to kill without it, it saves on weapon durability, which isn’t useless.

I’m not saying that Jugdral crits have no place or are strictly worse in every way, since I don’t really have much experience with them. But if you go into the real gameplay scenarios where GBA crits are supposedly a problem, you very quickly realise that not much of the cons hold up too well.

Also completely unrelated but

@Shrimperor

But crits in general have never been done well in the series imo. Both 3x Mt and 2xAtk - Def can make a 1% ruin a whole hour of progress.

Really the crit formula here isn’t the issue. On a surface level, yes, but the easier solution is just to make enemies unable to crit your player units by not giving them 5 crit weapons or excessive skill, or too many player units super low luck. Just because IS refuses to do it doesn’t mean it’s not a good solution .

[StreetHero]